Provavelmente você já ouviu falar sobre números primos, mas você sabe o que são e como identificá-los?
Essa sequência numérica bastante comum nas aulas de matemática, costuma causar espanto em quem não tem muita familiaridade com os números. Mas, afinal, o que é um número primo?
Se você chegou aqui sem nem saber o que é um número primo, não se preocupe. Neste artigo, vamos explicar tudo o que você precisa saber sobre essa sequência numérica.
O que é número primo?
Números primos nada mais são que números naturais que só podem ser dividido por apenas dois divisores: o número um e ele mesmo.
Confira alguns exemplos de números que são primos e que não são:
- O número 5 tem apenas dois divisores: 1 e ele mesmo. Isso significa que o 5 é um número primo.
- O número 6 tem mais de dois divisores, ou seja, 1, 2, 3 e 6. Isso significa que 6 não é um número primo, mas sim um número composto.
Agora, se tomarmos o exemplo do número 1, sabemos que ele tem apenas um divisor. Portanto, não pode ser um número primo, pois um número primo precisa ter obrigatoriamente dois divisores.
Como descobrir se um número é primo ou não
Existe alguns métodos para descobrir se um número é primo ou não. Vamos ver alguns deles:
1. Dividindo por outros números primos
Uma técnica bastante eficiente para descobrir se um número é primo ou não, é dividindo-o por outros números primos, sempre pela ordem (ex: 2,5,7,11, 17…).
Após realizar a divisão, precisamos interpretar os seguintes resultados:
- Se a divisão resultar em um número menor que o divisor e o restante não for igual a 0, ele é um número primo.
- Se o restante da divisão for igual a 0, então o número não é primo.
Para melhor entendimento, veja esse exemplo com o número 53.
O número 53 é um número primo?
Para verificar se o número é primo realizamos divisões sucessivas pelos primeiros números primos até encontrarmos um quociente menor que o divisor com o resto diferente de zero.
- Dividindo por 2 – 53/2 é igual a 26, com resto 1
- Dividindo por 3 – 53/3 é igual a 17, com resto 3
- Dividindo por 5 – 53/5 é igual a 10, com resto 3
- Dividindo por 7 – 53/7 é igual a 7, com resto 4
- Dividindo por 11 – 53/11 é igual a 4 , com resto 9
O quociente da divisão de 53/11 é menor que o número divisor (4 é menor que 11), portanto 53 é um número primo.
E se o quociente da divisão tiver resto 0?
Nesse caso, o número não é primo. Veja um exemplo com o número 18.
Dividindo por 2 – 18/2 é igual a 9, com resto 0.
Como o quociente da divisão tem resto 0, logo sabemos que 18 não é um número primo.
2. Método do Crivo de Eratóstenes
Uma outra maneira de descobrir um numero primo é utilizando o Crivo de Eratóstenes. Essa metodologia foi criada pelo matemático grego Eratóstenes que viveu entre 285 e 194 a.C. . O método consiste em encontrar números primos a partir da construção de uma tabela. A seguir, veja o passo a passo de como criar o Crivo de Eratóstenes:
- Faça uma tabela e escreva os números de um intervalo, por exemplo de 1 até 100 ou de 1 até 1000, dependendo da sua necessidade.
- Risque na tabela todos os números que são múltiplos de 2, exceto o número 2 (4, 6, 8, 10, 12…).
- Risque todos os números que são múltiplos de 3, exceto o número 3 (6, 9, 12, 15, 18…).
- Risque todos os números múltiplos de 5, exceto o número 5 (10, 15, 20, 25, 30, 35…).
- Risque todos os números que são múltiplos de 7, exceto o número 7 (17, 21, 28, 35, 42, 49…).
- Os números que sobraram, e que não foram marcados na tabela são os números primos.
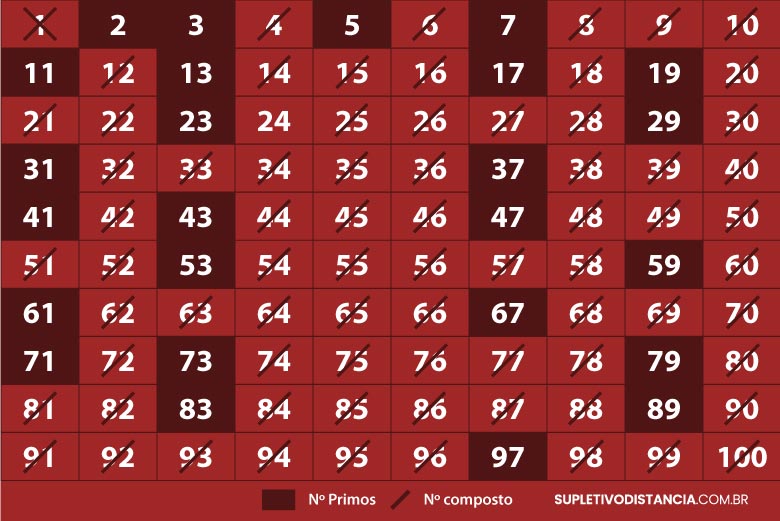
Números primos de 1 a 1000
Abaixo, veja os 168 números primos existentes entre 1 e 1000.
Entre 1 e 10 existem apenas 4 números primos. São eles:
2, 3, 5, 7
Entre 10 e 100 existem 21 números primos. São eles:
11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Do 100 até 200 existem 21 números primos. São eles:
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
De 200 a 300 existem 16 números primos. Sendo eles:
211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293
Do 300 a 400 existem 16 números primos. São eles:
307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397
Entre 400 a 500 existem 17 números primos. São eles:
401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499
De 500 a 600 existem apenas 14 números primos. Sendo eles:
503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599
DO 600 a 700 existem 16 números primos. São eles:
601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691
Entre 700 a 800 existem 14 números primos:
701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797
De 800 a 900 existem 15 números primos. Sendo eles:
809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887
E do 900 a 1000 existem 14 números primos:
907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
Curiosidades
Veja algumas curiosidades a respeito dos números primos.
- O número 1 é o único número que não é primo, pois seu único divisor é 1.
- Todos os números primos dessa sequência numérica serão obrigatoriamente ímpares, com exceção do número 2 que é o único número primo que é par.
- Ainda com exceção do 2 e 5, os demais números primos irão terminar nos algarismos 1, 3, 7 ou 9.
- Até a presente data, o maior número primo já descoberto possui mais de 23 milhões de dígitos e foi descoberto pelo engenheiro elétrico norte-americano, Jonathan Pace, de 51 anos.
Gostou dese artigo? Então compartilhe esse conteúdo nas suas redes sociais para que os seus amigos também tenham acesso a essas informações.
Siga-nos no Facebook e Twitter e fique ligado em todas as novidades!
Veja também: Como decorar a tabuada: Guia passo a passo para NUNCA mais ESQUECER


